 軽登山講座────伊藤幸司
軽登山講座────伊藤幸司
*この講座はBIGLOBE(NECビッグローブ)が公式に設置したstation50において2005年から2010年にかけて105回連載したものです。
【伊藤幸司の軽登山講座065】シミュレーションマップ12年(1)距離の把握――2008.9.25
*このシリーズは全4回で、(1)距離の把握、2)傾斜の把握、(3)行動時間の把握、(4)行動の量/質の把握――となります。
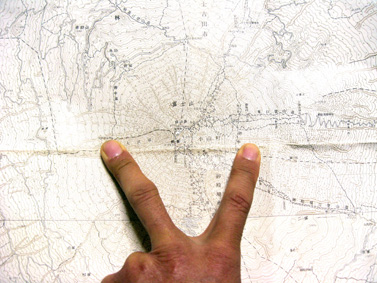
■5万分の1の富士山頂
5万分の1地形図の富士山にVサインによる10cmのモノサシを当てると、御中道の直径がちょうど5kmだということがわかる。巨人になった気分で富士山に目を近づけていく。
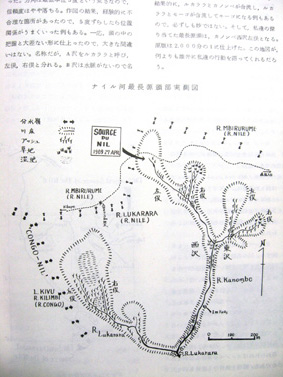
■ナイル河の最長源頭点を証明しようとした地図
ビクトリア湖に注ぐ最長河川のカゲラ川をルワンダ政府の25万分の1地図で計測、支流のルカララ川を選んで、その源流地帯を実測測量した。
●5万分の1から2万5000分の1へ
わかりやすく、東京オリンピックの頃といっておこう。地図の先進国英国では25万分の1、5万分の1、2万5000分の1、1万分の1の縮尺の地形図が新シリーズとして刊行されつつあった。
日本だって20万分の1、5万分の1、2万5000分の1、1万分の1が新シリーズとして準備されつつある時期だった。
なんだ、彼我の差はそう大きくないじゃないかというのは大間違い。英国ではクォーターインチマップ(25万3440分の1)、ワンインチマップ(6万3360分の1)、6インチマップ(1万560分の1)がとっくの昔に展開されており、第2次大戦後に刊行された2万5000分の1(アバウト2.5インチマップ)の初代シリーズもすでに1956年には全国をカバーしていた。
ここで注目しておきたいのは地図の先進国が最初に選んだ地形図の縮尺だ。「1インチ図」というのは図上の1インチ(2.54000cm)が実際の1マイル(1.60934km)を表すというもの。同様に「1/4インチ図」は図上の1/4インチが……、「6インチ図」は図上の6インチが……、というふうになる。
英国の陸軍陸地測量部が最初に考えたのが「1マイル」という距離を地図上に実感的に縮尺表示しようとしたことだった。
東京オリンピックのころ、学生だった私は「5万分1地形図」を使っていた。そのとき地図の縮尺を感覚的にとらえるために使った手は、指でVサインをつくって、それをめいっぱい広げて10cmのモノサシにした。5万分の1の地図上ではそれが現実の5kmを指していた。
地形図の上にVサインをかざすことで距離がつかめる……というよりは、空間のサイズ、縮尺感がつかめる、感じがした。正確なスケール(距離目盛り)は地図の隅についていたから、それで長さは測れたけれど、自然の中に直線的なものはほとんどないから、役に立つといえば立つけれど、立たないといえば立たなかった。
5万分の1地形図は明治時代に参謀本部の陸地測量部によって国土全体の三角測量から始められ、第二次世界大戦までにおおよそ完成したのだが、戦中戦後に撮られた米軍の航空写真によって道路や鉄道、町並みや建造物を修正した戦後の応急修正版というので私は育った。
(旧)建設省の国土地理院が自前の航空写真(正式には空中写真という)を図化機にかけて地図を描き出す空中写真測量を行い、全国を2万5000分の1地形図で覆うとする新しい国土基本図の登場は東京オリンピック以降のことだ。私はだから、5万分の1地形図で育ったが、途中で2万5000分の1地形図に切り替えることになった世代といえる。
ところがそれが問題で、2万5000分の1の縮尺でVサインの10cmが2.5kmになることはわかっても、その空間把握感、縮尺感がどうしても体に入ってこない。いちいちモノサシを当てて、縮尺換算して納得しないといけないのだ。地図上にV字サインを掲げることで見えていた(と思っていた)5万分の1の縮尺風景は、どちらかといえば錯覚に近いものだったように思う。
雑誌『岳人』(東京新聞出版局)で「五万分一地形図『富士山』を歩く」という連載(16回)をし、単行本『富士山・地図を手に』として刊行されたのが1980年。同じ年に山と溪谷社から『地図を歩く手帳』が出た。どちらも5万分の1図をメーンにしながら、2万5000分の1も視野の中に入れている。
今回読み直してみると『地図を歩く手帳』に次のような一文があった。
――
地図の使い方に2つの方向が出てきます。ひとつは4キロとか1マイルを縮小して、巨人の目で見下ろしたような見方をするもの。もうひとつは、目の前にひろげた地図そのものを現実のものとして直視し、必要に応じて長さや面積を原寸に換算するという使い方です。私見ですが、「読図」というレベルがあるとすれば、この2方向からのアプローチを、どこまで有効に組み合わせて利用しえているかということだと思うのです。
さて、4キロ=8センチというスケールで地図を見ていくとします。この場合4キロという現実の長さは「歩いて1時間」という体験によって把握されているわけです。つまり単純な長さではなくて、時間というファクターが加えられているわけです。
ということは、図上で8センチの長さをたどるときにも時間を無視するわけにはいかないはずです。そこでもし時間も5万分の1に縮めてみると、14分の1秒になります。しかしそれでは図を読むどころか、見ることさえ不可能になります。かといって、図上の8センチを1時間かけてたどるというのも、無意味なことはすぐにわかります。
そこで適当な時間、たとえば8センチを1分(60分の1)とか10分(6分の1)としてみます。1日の行程を20キロとすれば、それを図上では5分なり50分でたどってみるわけです。
しかしほんとうのところ、時間というのは縮尺できるものなのか、という疑問がでてきます。4キロを1時間かけて歩いている場面を思い起こしてみます。もし道草をしたりせずに歩きつづけていたとしても、ゆっくりと変化していく風景のなかに見るべきものはたくさんあります。集落があり、森があり、耕地があり、人の姿があり、そういったものの外観からでも、観察は時間を越えて過去や未来の姿にまでおよんでいきます。その土地の気候や、そこに住む人々の懐ぐあいまで見抜こうとしていることにも気づきます。
現実の1時間というのは、そういう体験を含んでいるのです。ですからそれを1分や10分でたどってみても、旅のおもしろさはほとんど味わうことはできません。となれば、1分でも10分でも、短い時間だからといって退屈でないとはいえません。
そこで地図の上でも、観察や思索の時間をたっぷりとってやります。もうお気づきのことと思いますが、その種の時間にはいかなる縮尺もありえません。
巨人の目を、地図そのものをはいずりまわるミクロ人間の目に切り替えてみるわけです。ミクロ人間はスーパー・マンですから、ヤブ山であろうと岸壁であろうと、たじろぐことなく、山の向こうの、現実の旅では見えないところにまで足をのばしていくのです。それはちょうど、図化機によって作りだされた立体(写真)画像の地表面をはっていくフローティング・マークとよばれる極小の球のようなものでしょう。
その分身としてのミクロ人間が切りひらいた地図上の道を、私たちは巨人の目で追い、必要なら色エンピツでたどっていくこともできるのです。
地図上での直線踏破は、そういった、時間をかけた旅への有効な切り口になるだろうと思うのです。まず、直線に交わってくる等高線を1本、1本越えていきます。5本目ごとの計曲線のところで標高をチェックしておくと高度感もわかりますし、その手作業によって傾斜感がつかめてきます。つまり、等高線の並び方のパターンが、はっきりと見えてきます。
そしてちょっと道草を食ってみれば、いくつかのタイプのちがう傾斜面が組み合わさって、土地の起伏がかたちづくられていることがわかります。しかもそれらの傾斜面は、かなり明瞭な境界によって互いに繋ぎ合わされているのです。山地の末端などはそのもっともよい例ですが、ひとつづきの集落でも、その上部と下部とでは、斜面の性質が変わっていることがよくあります。
集落や耕地のひろがり方、道路の敷かれ方、川の流れ方なども注意して見ていくと、ある特定の斜面と強く結びついていることがわかりますが、むしろその原則からはみ出ているおかしなところから、疑問が疑問を生むような、推理遊びがはじまることが多いようです。
――
この『地図を歩く手帳』がきっかけになって、1983年から、私は朝日カルチャーセンター横浜の「40歳からの登山入門講座」に地図担当講師として参加することになった。これは5人の講師による講座があり、それに実技登山がくっつくというかたちで1995年までに40回実施された。私が「中高年登山」に関わるのは、これによる。
●距離を測る
地図に興味のある方は「マップメーター」をご存じだろう。回転式距離目盛りが小さな車輪と連動していて、地図の上を走らせると縮尺に応じた距離を表示するというものだ。正式には曲線計(curvimeter)といってカーヴィメーターと読むのが妥当と思われるが、日本ではキルビメーターという名で通用する。
曲がりくねった道の距離を測るにはこのマップメーターが便利……ということで私ももちろん買ったことがあったけれど、いまはどこにいったやら。
多くの人が便利だと思って買っているのではないかと思うけれど、A地点からB地点までのあらかじめ定めた2点間の距離を測るための道具といえる。途中で距離をチェックしようとするとあんがいむずかしい。
地図上の2地点間の距離を計るだけなら地図の見え方に異変はないが、その2点間に距離目盛りを入れていくと、地図の縮尺感がガラリと変わることに気がついた。
わかりやすくいえば、5万分の1図でも2万5000分の1図でも、道筋に1kmごとの目盛りを入れていくと、両方を並べて同時に見比べても縮尺による空間把握に混乱が生じない。
登山用の地図がバラバラの縮尺にもかかわらず違和感なく使われているのは、そこに「所要時分」というコースタイムが入っているからだ。あれを頼りにすることができなかったら、縮尺をそろえてくれないと使い物にならない。
つまり、登山地図にとって、あのコースタイムが地図としての生命線になっている。コースタイムの算定に関して客観的な基準や計算方法を示せなくても、そこに確固とした数値を入れておかなくては屋台骨が崩れてしまう……ということに気がついた。
私はそこで、地形図上で、歩く予定のルートに距離目盛りを入れることを試みた。
2万5000分の1地形図では4cmが1km、4mmが100mとなるので、ディバイダー(divider。円を描くコンパスとちがって両方とも針になっている)の両脚を4mm開いて、歩幅100mで道を歩いていくという計り方をしてみた。10歩で1kmだから、ペンで印を付けていくと「地図上を歩く」という気分も味わえる。
朝日カルチャーセンター横浜での地図の講義ではそのためにわざわざディバイダーを用意してもらうのは大げさだった。地図の本には、曲がりくねった道に糸をはわせれば長さが計れるとある。うまくはわせられない場合には糸を湿らせるといいなどと親切なアドバイスもあるけれど、いずれもあらかじめ決めた2点間の距離を計る方法だ。
ディバイダーによる計測は「地図を歩く」という素朴さに最も近いという意味で私には究極の方法と思えたが、その代用が後に大きな展開を見せてくれる。
代用策とは、親指の幅ほどの紙片を切り取って、地図の縮尺表示の目盛りを写し取って、その紙片を地図の上で曲線に沿わせながら(ペン先で軽く押さえると方向転換しやすい)500mとか1kmの目盛りを振っていく。1987年の『初めての山歩き』(主婦と生活社)はかなりのロングセラーとなったが、そこではこう紹介している。
――
たとえば紙片の先を1センチ程度の幅にして、そこに4ミリ間隔のふたつの点を記しておく。その紙片を片手に持って登山ルートに当てながら、ペンで4ミリごとの点を打っていく。道がカーブしていたり、ジグザグになると正しく計れないが、目見当で調整していけばいい。誤差を気にしないで進めていく。
5万分の1の地図であれば地図上の4ミリは現実の200メートル、2万5000分の1では100メートルになる。いずれも1キロごとに数字を入れていく。
ついでに周囲も眺める。道が分岐していないか、「しの地」「荒地」「はいまつ地」などの記号があるかどうか。三角点や水準点はないか、高圧電線は近くを通っていないか、キョロキョロと見る。道筋に現れる地名なども読んでいく。読んだものを蛍光マーカーなどでチェックしておいてもいい。さらにコースを横切る等高線のうち、太い計曲線だけを拾って色を着けておく。
こうすると道筋に1kmごとの数字が入り、必要ならさらに細かい距離を読むこともできる。登りがおよそ何キロあるかがわかるだけでなく、緩い登りが何キロか続いた後、尾根筋がはっきりしてしてくるとか、頂上直下の急登がおよそ何キロかといったことがわかってくる。途中の小屋がコースの何分の一のあたりかという見当もつく。
――
そのページの脚注として次のように書いている。
――
登山道に距離目盛りを入れたら、高度の変化を等高線から読み取ることによって、その傾斜を計ることができる。水平距離を分母とし、垂直距離を分子とする値を三角関数真数表の tan(タンジェント)の項から探せばいい。
100メートル行って100メートル上がったとすると、その平均傾斜は45度、100メートルの間に約60メートル登ったとすると30度の傾斜である。
――
しかし、山歩きの入門編で、登山道の距離を計るという提案は、知識のある登山者からはバカにされたにちがいない。無理というよりアホだと思われたにちがいない。
たとえば登山道は「幅員1.5m未満」の道路として描かれる。破線で描かれるその線の太さは0.2mmと決められている。2万5000分の1の地図上の0.2mmは現実には5mとなるから線の太さそのものが車の通れる道幅になっている「幅員1.5m未満」どころではない。急斜面のジグザグなどは、完全にその道幅の中に含まれてしまうので、地図に描かれた登山道そのものが、実際の登山道の長さをかなり省略したものとなっている。
しかも、登山道の表記では、急斜面のジグザグを表現として描いていることがあるけれど、その場合は実際の何倍もの大きなジグザグになってしまう。地図上で登山道をどんなに精密に計っても、根元的な誤差を埋めることは不可能なのだ。すなわち、登山道の距離を地図上で計るというのはナンセンスということになる。
ところが私はもともと山屋ではなくて、川屋だったから、不確実な地図情報でも計ることに意味があるという立場にあった。
1968年から翌年にかけて早稲田大学探検部の第一次ナイル河全域踏査隊として、ルワンダ共和国のルカララという名の川の源頭部を「ナイル河最長源頭点」であろうと報告した。当時は世界の大河は(1)ミシシッピー 6,530km、(2)アマゾン 6,200km、(3)ナイル 5,760km)とされていた。理科年表の1969年版までのものだから、教科書などもその数値を採用していた。
ご存じのように、アメリカのミシシッピー川はショートカット工事によって短縮し、ナイル川はビクトリア湖より上流部も加えることによって長さを増した。1970年版の理科年表では(1)ナイル 6,690km、(2)アマゾン 6,300km、(3)ミシシッピー 6,210kmと数値も順位も大きく入れ替わった。
私たちの「最長源頭点」の探査は、最後のところで自分たちの簡易測量による地図を添えて終了したが、基本的には河の長さはすべて地図によって計られてきた。詳しい地図が作られれば河の長さは長くなる。長くなる可能性を残しているのはアマゾン河だったから、いずれはナイル河はその地位を明け渡すことになると予想しての行動だったが、衛星写真で計ればすぐにでも逆転劇が起こりそうなことが現在までもう40年近くも放置されてきたのは、英国の王立地理学会などの権威による判定がなされていないからだろう。
登山道を実測している人がいるそうだが、私は長さを地図で計るということに疑念はもたなかった。知りたかったのは誤差がどれほどあるのかということだった。
1989年に朝日新聞社から『ふれあいの「首都圏自然歩道」』というガイドブックがでた。環境庁主導の「首都圏自然歩道」(全144コース、全長1,667km)の全ルート完成に合わせたもので、私は埼玉・群馬・栃木・茨城の4県を担当した。もちろん自分で歩く余裕はないので、仲間を車で運んでは回収して、キャンプ地でデータ収集を行うという手配師を担当した。
それぞれのコースには距離表示がなされていて、コース中にも距離数を入れた道標が設置された。コースのほとんどは平坦な道だけれど、登山道というべき部分もあって、そこで私が地形図上で計った距離と比べていくと、車で走れる道に関してはほとんど誤差はなく、ジグザグ道の登山道では最大20%の誤差(短くなる)という結果が出た。
最大20%短いということは私にとっても大きな問題ではあったが、距離目盛りを入れておくことで地形図の「距離感」が圧倒的に向上することが重要だということで目をつぶることにした。のちに20%の誤差が自動的に5%の誤差に縮小するというマジックを発見するのだが、そのことは第3回目のテーマになる。
★目次に戻ります
★トップページに戻ります

